圆球体积的公式
〖1〗、圆球体积的计算公式为:V = r。详细解释如下:圆球体积的计算涉及一个数学概念,即球的体积公式。在这个公式中,V 代表球的体积,r 代表球的半径。而符号 是一个常数,大约等于 14159。这一公式反映了球体积与其半径之间的数学关系。
〖2〗、圆球体积的计算公式为:V = r。圆球体积的计算公式是一个重要的几何公式,用于计算三维空间中球体的体积。这里的是一个数学常数,约等于14159,r代表球的半径。具体解释如下: 体积公式的基本形式:在三维几何中,圆球体积的计算公式为V = r。
〖3〗、计算圆球的体积公式为:V = r,其中r是圆球的半径。圆球的体积计算涉及数学中的立体几何知识。具体解释如下: 体积公式介绍:圆球的体积计算公式为V = r。这个公式中,是一个数学常数,约等于14159;r代表圆球的半径。
〖4〗、圆球体积公式:V = r^3 圆球面积公式:A = 4r^2 下面对这两个公式进行 圆球体积公式解释 体积是三维空间中物体所占空间的大小。圆球的体积公式是通过对球体内部空间进行几何分析得出的。公式中的r代表圆球的半径,是一个数学常数,约等于14159。
〖5〗、圆球体积的公式是V=(4/3)πr,其中r是圆的半径,π是圆周率,约等于1415926。这个公式可以用来计算圆球的体积,其中r是圆球的半径。圆球体积公式的推导过程如下:首先,考虑一个平面内截取的圆,其面积为πr。当我们截取这个圆的三个维度时,我们得到了一个立方体,其边长为r。
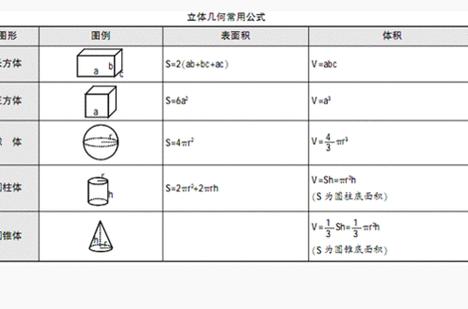
圆球体积公式的推导过程?
圆球的体积公式为V = r^3,其中r为球的半径,为圆周率。这个公式的推导过程主要基于几何学和微积分的知识。推导过程解释: 基础知识准备:首先,我们需要知道球体的一些基本属性。球体是一个三维的几何体,所有的点都离其中心有固定的距离,也就是半径r。
圆球体积公式的推导过程如下: 构造辅助几何体: 考虑一个底面半径为R,高也为R的圆柱体。 从这个圆柱体中挖去一个等底等高的圆锥。 剩余部分与半球的关系: 剩余部分的体积与一个半球的体积相等。
即半球的体积,公式为V = 2/3πR^3。因此,整个球的体积就是半球体积的两倍,即V = 4/3πR^3。这个结论是基于球是由圆旋转形成的,圆的面积S = πR^2。如果我们将圆的面积看作是球体积的积分,根据积分的原理,我们就能得到球的体积公式V = 4/3πR^3。
圆球的体积计算公式为V = r。这个公式中,是一个数学常数,约等于14159;r代表圆球的半径。通过这个公式,我们可以根据已知的半径计算出圆球的体积。 公式推导过程:这个体积公式是基于几何学和数学原理推导出来的。圆球是一个三维的立体图形,其每一个点都距离球心等距。
球的体积:4/3πR^3 推导过程:比较好拿纸笔画好图 第一步:先想象一个半球(高R,底面半径R,这个应该能理解吧),在距它底面L处,做一个横截面。
推导圆球的体积和表面积计算公式的过程是这样的:假设圆球的半径和圆柱的底面半径相等,都为r,则圆柱的高是2r,或者是d,再用字母和符号表示出圆柱的体积和表面积计算公式,然后分别乘 ,就得出圆球的体积和表面积,最后进行总结。

球体体积公式的推导过程
球体体积公式为 V = r,其中r为球体的半径,是圆周率。这个公式的推导过程如下:球体体积公式推导 几何直观法推导 球体可以被视为无数个以球心为中心、半径相同的圆片叠加而成。当这些圆片无限多时,即可形成一个连续的体积。
球体体积公式推导过程:v=4/3×πr^3。欲证v=4/3×πr^3,可证1/2v=2/3×πr^3。做一个半球h=r,做一个圆柱h=r。V柱-V锥=π×r^3-π×r^3/3=2/3π×r^3。若猜想成立,则V柱-V锥=V半球。
球的体积公式为V = r。其推导过程如下:引言 球的体积公式是通过积分几何的方法推导出来的。这种方法基于微积分的基本原理,通过对球体的几何形状进行分割和近似,从而计算出其体积。推导过程 分割球体:将球体分割成许多小的圆柱体。
球体积公式:推导方法:左右是夹在两个平行平面间的两个几何体(左图是半径为R的半球,右图是一个中间被挖去一部分的圆柱,其中,圆柱底面半径为R,高为R,挖去部分是一个圆锥,底面半径为R,高为R)。
球的体积公式V=4/3πR3的推导过程是这样的:首先,设想一个圆柱体,其底面半径为R,高度同样为R。然后,从这个圆柱体的中心部分挖去一个与之等底等高的圆锥体。剩下的部分与一个半球体相比较,它们在任何截面上的面积都是相等的。由此,我们可以得出结论,这两个几何体的体积也是相等的。
球体体积公式为V = πr,其中r是球体的半径,π是圆周率。推导过程如下:球体体积公式的表达 球体体积公式V = πr,是一个描述球体内部空间大小的数学表达式。其中,π表示圆周率,r代表球体的半径。这个公式用于计算球体的体积。

球体的体积是怎么推导出来的?
〖1〗、由V半球可推出V球=2×V半球=4/3×πr^3 证毕。
〖2〗、几何直观法推导 球体可以被视为无数个以球心为中心、半径相同的圆片叠加而成。当这些圆片无限多时,即可形成一个连续的体积。我们可以设想这样一个过程:从最外层开始,逐渐向内叠加每一层圆片的面积,直至整个球体。
〖3〗、球的体积公式为V = r。其推导过程如下:引言 球的体积公式是通过积分几何的方法推导出来的。这种方法基于微积分的基本原理,通过对球体的几何形状进行分割和近似,从而计算出其体积。推导过程 分割球体:将球体分割成许多小的圆柱体。
〖4〗、由于圆锥体的体积可以很容易地计算出来,它是圆柱体积的1/3,即V=1/3πR3。因此,剩下的部分,即半球体的体积为V=2/3πR3。由此,我们可以推断出整个球体的体积为2倍的半球体积,即V=4/3πR3。实际上,球体也可以通过旋转一个圆得到。圆的面积为S=πR2。
〖5〗、球体体积公式推导过程如下:首先,球的半径设为R,球的表面积公式为F=4πR2。接着,将球体分割成n个等分的多棱椎体,每个多棱椎体的底面积为ΔF,顶点位于球心。每个多棱椎体的体积计算公式为ΔV=RΔF/3。因此,球体的总体积V可以通过求和计算得出:V=R/3*Σ[1,N]ΔF。
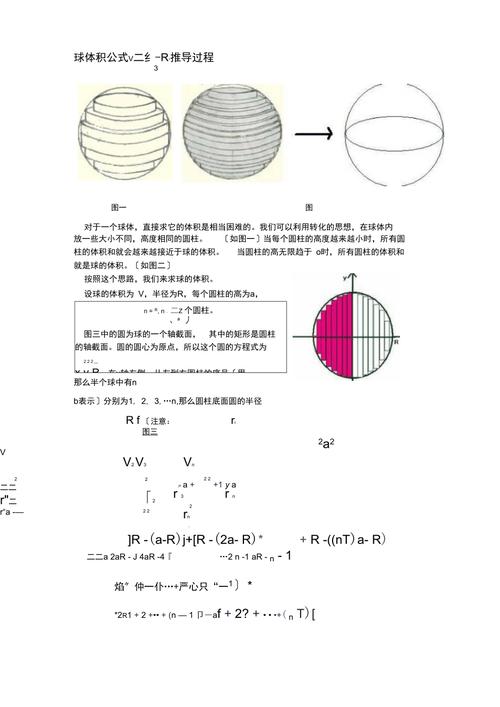
球的体积公式是怎么样推导的?
球的体积公式V=4/3πR3的推导过程是这样的:首先,设想一个圆柱体,其底面半径为R,高度同样为R。然后,从这个圆柱体的中心部分挖去一个与之等底等高的圆锥体。剩下的部分与一个半球体相比较,它们在任何截面上的面积都是相等的。由此,我们可以得出结论,这两个几何体的体积也是相等的。
由V半球可推出V球=2×V半球=4/3×πr^3 证毕。
球体积公式:推导方法:左右是夹在两个平行平面间的两个几何体(左图是半径为R的半球,右图是一个中间被挖去一部分的圆柱,其中,圆柱底面半径为R,高为R,挖去部分是一个圆锥,底面半径为R,高为R)。
球的体积公式推导 球的体积公式为V = r,其中r为球的半径。这个公式可以通过积分法推导出来。以下是详细的推导过程:基本思路 推导球的体积公式,可以通过对半球进行积分来实现。半球可以看作是一个由无数层圆环组成,每一层圆环的面积随着距离球心的距离增加而增大。
球的体积公式为V = r。其推导过程如下:引言 球的体积公式是通过积分几何的方法推导出来的。这种方法基于微积分的基本原理,通过对球体的几何形状进行分割和近似,从而计算出其体积。推导过程 分割球体:将球体分割成许多小的圆柱体。